決定木とランダムフォレストによるデータ分類

Contents

決定木とは
データの説明
サンプルコード（決定木）
ランダムフォレストとは
サンプルコード（ランダムフォレスト）
コード全文（決定木）
コード全文（ランダムフォレスト）

決定木とは

決定木とは，その名の通り木のような形をしているアルゴリズムです．例として，下図を見るとイメージが湧きやすいかと思います．

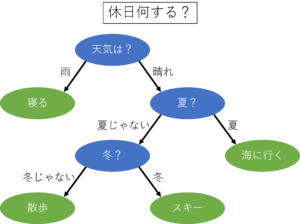
上に示した決定木は，休日に何をするかを決める決定木の例です．決定木では，いろいろな選択肢（基準）のもとに，最終的に答えが決まります．

選択肢（基準）を決める方法としては，CART法というアルゴリズムが多く使われています．CART法では，最もよくデータを分類する基準を探して分岐を設定します．数学的にデータを最もよく分類する基準としてはジニ係数が多く使われます．ジニ係数の詳細はWikipedia参照としますが，この値がより低くなるように設定することで，最もよくデータが分類できます．

それでは，実際に決定木を用いた分類を，コードを見ながら確認していきます．

データの説明

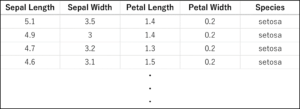
今回は機械学習用データセットとしてよく使われるアヤメのデータセットを用います．以下の表にその一部を示します．150件のデータがSetosa, Versicolor, Virginicaの3品種に分類されており，それぞれ，Sepal Length（がく片の長さ）, Sepal Width（がく片の幅）, Petal Length（花びらの長さ）, Petal Width（花びらの幅）の4つの特徴量を有しています．今回は，これらの特徴量から品種を推定・分類することを目指します．

サンプルコード（決定木）

以下，決定木を用いたサンプルコードです．途中途中で説明をはさみながらコードを載せていきますが，ページ下部にコード全体をもう一度記載しておきます．

#-*- coding: utf-8 -*-
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn import tree

#-*- coding: utf-8 -*-

from sklearn.datasets import load_iris

from sklearn.model_selection import train_test_split

from sklearn import tree

Pythonの機械学習用ライブラリのひとつであるscikit-learnを用いて，決定木による分類を行います．scikit-learnにはすでにアヤメのデータセットが用意されています．1行目のコードでアヤメのデータセットをインポートしています．データセットのうち，いくつかは学習に用いて，残りは精度の評価に用います．2行目のコードでデータセットを分けるための関数をインポートしています．3行目のコードは，scikit-learnで決定木を扱うための関数，treeをインポートしています．

iris = load_iris()
X = iris.data
y = iris.target

iris = load_iris()

X = iris.data

y = iris.target

まず，変数irisに，インポートしたアヤメのデータセットを代入しています．さらに，代入したデータの中から，特徴量を示すデータiris.dataを変数Xに代入します．また，品種を示すデータiris.targetを変数yに代入します．ここで，変数X，yの中身を確認してみましょう．

print (X[0:5,:])
print(y)

1 2	print (X[0:5,:]) print(y)

Xは中身が多いので最初の5行だけ表示します．実行すると，以下のような結果が得られます．

[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]]

[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2]

Xの中身は，最初に示した特徴量の表と同じ値になっていることがわかります．yの中身は0，1，2が表示されています．それぞれの数値がSetosa, Versicolor, Virginicaの品種を表しています．

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

1	X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

test_sizeの指定により，Xとyの中身を，学習用7割，テスト用3割に分けます．random_stateはデータを分割する際の乱数のシード値で，こうすることで誰がやっても毎回同じように分類されます．

clf = tree.DecisionTreeClassifier(max_depth=3)
clf.fit(X_train, y_train)

1 2	clf = tree.DecisionTreeClassifier(max_depth=3) clf.fit(X_train, y_train)

clfに，今回学習に用いる決定木を定義します．ここで，決定木の深さをmax_depthで定義しています．この値が小さすぎるとうまく判別できなかったりしますが，深さが大きすぎても，今度はトレーニングデータに過剰に適合した過学習に陥る場合があるので注意が必要です．つづいて，clf.fitで学習を開始することで，トレーニングデータに適した判別条件が設定されます．

print (clf.score(X_test, y_test))

1	print (clf.score(X_test, y_test))

学習した決定木を用いて，テストデータの判定を行います．判定した結果の正解率を表示すると以下のようになります．

0.9777777777777777

だいたい98%の正解率であることがわかります．せっかくなので，ほんとにそうなっているかの確認も兼ねて判定結果の中身も見てみましょう．まずは，判定に用いるテストデータ（今回は150個うちの3割なので45個）の中身を確認します．

print(y_test)

1	print(y_test)

上のコードを実行すると，以下のように表示されました．

2 1 0 2 0 2 0 1 1 1 2 1 1 1 1 0 1 1 0 0 2 1 0 0 2 0 0 1 1 0 2 1 0 2 2 1 0 1 1 1 2 0 2 0 0

つぎに，学習させた決定木の判定結果を見てみましょう．

print(clf.predict(X_test))

1	print(clf.predict(X_test))

判定を行う場合にはpredictを用います．さて結果は…

2 1 0 2 0 2 0 1 1 1 2 1 1 1 1 0 1 1 0 0 2 1 0 0 2 0 0 1 1 0 2 1 0 2 2 1 0 2 1 1 2 0 2 0 0

ほとんどすべて正解していますが，38個目の1（Versicolor）だけ2（Virginica）だと誤判定しています．きっと，どちらともつかない微妙な特徴量だったんでしょう．45個中44個正解しているので，確かに正解率は約98%ですね．

ここで，アヤメのデータセットに対して全体的にどの程度の正解率を出すことができるのか確認するため，K分割交差検証を行います．今回はK=10として，データを10分割してそれぞれの結果を見てみます．

from sklearn.model_selection import StratifiedKFold, cross_val_score
import numpy as np
stratifiedkfold = StratifiedKFold(n_splits=10)  #K=10分割
scores = cross_val_score(clf, X, y, cv=stratifiedkfold)
print('Cross-Validation scores: {}'.format(scores))   # 各分割におけるスコア
print('Average score: {}'.format(np.mean(scores)))  # スコアの平均値

from sklearn.model_selection import StratifiedKFold, cross_val_score

import numpy as np

stratifiedkfold = StratifiedKFold(n_splits=10) #K=10分割

scores = cross_val_score(clf, X, y, cv=stratifiedkfold)

print('Cross-Validation scores: {}'.format(scores)) # 各分割におけるスコア

print('Average score: {}'.format(np.mean(scores))) # スコアの平均値

StratifiedKFoldはK分割するための，cross_val_scoreは分割したデータで精度を検証するための関数です．さて，結果は以下のようになりました．

Cross-Validation scores: [1. 0.93333333 1. 0.93333333 0.93333333 0.93333333 0.93333333 0.93333333 1. 1. ]

Average score: 0.96

交差検証の結果によると，平均して96%の正解率を出すことができています．

ランダムフォレストとは

ランダムフォレストでは，複数の決定木を用いて学習を行います．そのとき，元の学習データからランダムにデータを選択し，個々の決定木を生成します．そして，実際に未知のデータを評価する際には，個々の決定木が下した結論を多数決することで全体の結論とします．

決定木はとても分かりやすいアルゴリズムですが，データによっては望ましい木構造が生成できなかったり，過学習を起こしやすかったりすることで知られています．一方，ランダムフォレストはその特性上個々の決定木間の相関が低くなるので，決定木に比べて過学習の影響を非常に小さくできるメリットがあります．以下に，上記で用いたアヤメのデータセットをランダムフォレストで解析した場合のサンプルコードを示します．

サンプルコード（ランダムフォレスト）

基本的な流れは決定木と全く同じなので，異なる箇所のみ解説します．

#-*- coding: utf-8 -*-
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier

#-*- coding: utf-8 -*-

from sklearn.datasets import load_iris

from sklearn.model_selection import train_test_split

from sklearn.ensemble import RandomForestClassifier

今回はランダムフォレストを用いるので関数RandomForestClassifierをインポートしています．

iris = load_iris()
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

clf = RandomForestClassifier(max_depth=3, random_state=0)
clf.fit(X_train, y_train)

iris = load_iris()

X = iris.data

y = iris.target

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

clf = RandomForestClassifier(max_depth=3, random_state=0)

clf.fit(X_train, y_train)

ここではもちろんランダムフォレストの関数を用いています．ランダムフォレストで学習に使うデータは学習データ全体の中からランダムに選定されますが，random_state=0によって，誰がやっても毎回同じように選定されます．このとき，n_estimatorsを指定すれば木の本数も変えられますが，今回はデフォルトのまま行います．ちなみにデフォルトの本数は10本です．

print (clf.score(X_test, y_test))

1	print (clf.score(X_test, y_test))

ランダムフォレストでの学習結果を用いて，テストデータの判定を行います．判定結果の正解率は以下のようになります．

0.9333333333333333

だいたい93%の正解率であることがわかります．ここで，決定木の場合と同様に，K=10として，K分割交差検証を行います．

from sklearn.model_selection import StratifiedKFold, cross_val_score
import numpy as np
stratifiedkfold = StratifiedKFold(n_splits=10)  #K=10分割
scores = cross_val_score(clf, X, y, cv=stratifiedkfold)
print('Cross-Validation scores: {}'.format(scores))   # 各分割におけるスコア
print('Average score: {}'.format(np.mean(scores)))  # スコアの平均値

from sklearn.model_selection import StratifiedKFold, cross_val_score

import numpy as np

stratifiedkfold = StratifiedKFold(n_splits=10) #K=10分割

scores = cross_val_score(clf, X, y, cv=stratifiedkfold)

print('Cross-Validation scores: {}'.format(scores)) # 各分割におけるスコア

print('Average score: {}'.format(np.mean(scores))) # スコアの平均値

結果は以下のようになりました．

Cross-Validation scores: [1. 0.93333333 1. 0.93333333 0.93333333 0.93333333 0.8 0.93333333 1. 1. ]

Average score: 0.9466666666666667

交差検証の結果によると，平均しておよそ95%の正解率を出すことができています．

コード全文（決定木）

このページで紹介した決定木のコード全文を載せておきます．なお，関数などの呼び出しはコードの先頭にまとめ，途中で行った確認用のprint文などは省いています．

#-*- coding: utf-8 -*-
from sklearn.datasets import load_iris 
from sklearn.model_selection import train_test_split 
from sklearn import tree
from sklearn.model_selection import StratifiedKFold, cross_val_score 
import numpy as np 

iris = load_iris() 
X = iris.data 
y = iris.target

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

clf = tree.DecisionTreeClassifier(max_depth=3) 
clf.fit(X_train, y_train)

print (clf.score(X_test, y_test)) #正解率の表示

#K分割交差検証
stratifiedkfold = StratifiedKFold(n_splits=10)  #K=10分割 
scores = cross_val_score(clf, X, y, cv=stratifiedkfold) 
print('Cross-Validation scores: {}'.format(scores))   # 各分割におけるスコア 
print('Average score: {}'.format(np.mean(scores)))  # スコアの平均値

#-*- coding: utf-8 -*-

from sklearn.datasets import load_iris

from sklearn.model_selection import train_test_split

from sklearn import tree

from sklearn.model_selection import StratifiedKFold, cross_val_score

import numpy as np

iris = load_iris()

X = iris.data

y = iris.target

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

clf = tree.DecisionTreeClassifier(max_depth=3)

clf.fit(X_train, y_train)

print (clf.score(X_test, y_test)) #正解率の表示

#K分割交差検証

stratifiedkfold = StratifiedKFold(n_splits=10) #K=10分割

scores = cross_val_score(clf, X, y, cv=stratifiedkfold)

print('Cross-Validation scores: {}'.format(scores)) # 各分割におけるスコア

print('Average score: {}'.format(np.mean(scores))) # スコアの平均値

コード全文（ランダムフォレスト）

このページで紹介したランダムフォレストのコード全文を載せておきます．こちらも諸々のの呼び出しはコードの先頭にまとめています．

#-*- coding: utf-8 -*-
from sklearn.datasets import load_iris 
from sklearn.model_selection import train_test_split 
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import StratifiedKFold, cross_val_score
import numpy as np

iris = load_iris() 
X = iris.data 
y = iris.target 
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0) 

clf = RandomForestClassifier(max_depth=3, random_state=0) 
clf.fit(X_train, y_train)

print (clf.score(X_test, y_test))#正解率の表示

#K分割交差検証
stratifiedkfold = StratifiedKFold(n_splits=10)  #K=10分割
scores = cross_val_score(clf, X, y, cv=stratifiedkfold)
print('Cross-Validation scores: {}'.format(scores))   # 各分割におけるスコア
print('Average score: {}'.format(np.mean(scores)))  # スコアの平均値

#-*- coding: utf-8 -*-

from sklearn.datasets import load_iris

from sklearn.model_selection import train_test_split

from sklearn.ensemble import RandomForestClassifier

from sklearn.model_selection import StratifiedKFold, cross_val_score

import numpy as np

iris = load_iris()

X = iris.data

y = iris.target

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

clf = RandomForestClassifier(max_depth=3, random_state=0)

clf.fit(X_train, y_train)

print (clf.score(X_test, y_test))#正解率の表示

#K分割交差検証

stratifiedkfold = StratifiedKFold(n_splits=10) #K=10分割

scores = cross_val_score(clf, X, y, cv=stratifiedkfold)

print('Cross-Validation scores: {}'.format(scores)) # 各分割におけるスコア

print('Average score: {}'.format(np.mean(scores))) # スコアの平均値

決定木とは

データの説明

サンプルコード（決定木）

ランダムフォレストとは

サンプルコード（ランダムフォレスト）

コード全文（決定木）

コード全文（ランダムフォレスト）

KerasでMNISTの判定

Kerasで回帰

Google Colaboratoryの使い方