ロジスティック回帰とは
機械学習に取り組む前段階として,まずはロジスティック回帰を行ってみます.ロジスティック回帰の詳細はWikipedia参照.ものすごく大雑把(かつ不正確)に言うと,2クラス分類問題を解く手法です.これが不正確な表現ってわかる人は,既にわかっている人だと思います.ということで上の雑駁な表現をお許しください.
データの説明
データファイル
ここでの練習用に,データファイルを作りました.
また,以下のソースコードの全体像(jupyter notebook形式)と,データをまとめたファイルを圧縮して以下に置いておきます.
Example2.zip
特になんということもないデータです.完全に架空のデータです.左から2つの列は説明変数,一番右の列は被説明変数というイメージで,0か1かの2クラスに分かれています.

このデータを使ってやりたいこと
ここでやりたいことは,説明変数2つから,クラスが0か1かを当てたい,というものです.やり方は色々とあり,機械学習手法で次回以降解いていきたいと思いますが,まずは歴史のあるロジスティック回帰を用いて行う,ということです.
サンプルコード
以下,サンプルコードです.
|
1 2 3 4 5 |
# -*- coding: utf-8 -*- #上のコメントは,普通pythonで日本語を使うために必須.ただ,Google Colaboratoryでは無くてもOK? import pandas as pd #pandasはデータを扱うためのライブラリ import numpy as np #numpyは数値計算を効率的に行うための拡張 import matplotlib.pyplot as plt #matplotlibはグラフ描画用ライブラリ |
基本的にコメントをつけた通りですが、改めて。
最初の文章はおまじないのようなもので、これが無いと一般的にはpythonを動かす際に、日本語コメントが入っているとエラーを吐き出します。でも、Google Colaboratoryでは内部で処理してくれているようで無くても大丈夫なのですが、一応つけています。
3行目からは、ライブラリを使うための宣言です。Pandasはデータを扱うための、numpyは数値計算を効率的に行うための拡張です。両方とも(特にnumpyは)、今後多くのプログラムで利用します。matplotlibも同様に頻出のライブラリです。これらについてもおまじないのように書くのがいいです。
|
1 2 3 4 |
#Google Colaboratoryのみに必要.既存ファイルを扱うのだけは,Google Colaboratoryは不便です. #ファイルをアップロードするためのダイアログを出します. from google.colab import files uploaded = files.upload() |
上のコードは、Google Colaboratoryの場合にのみ必要なワンステップです。
サーバー上で解析を行うため、ローカルのファイルを読み込むことができません。対策は色々とあり、Google Driveにアップする方法などもあって場合によってはそちらが便利なのですが(というか、そっちにしないとできない場合もある)、今回のbinarize.csvのような小さなファイルを扱う場合にはこのくらいでも十分です。
上のコードを実行するとファイルを読み込むダイアログが出てきます。それに従いファイルを読み込むと、以下のような感じになります。
|
1 2 3 4 |
df = pd.read_csv('binarize.csv', header=None)#Google Colaboratoryにアップしたファイルを,このプログラムの中で使えるように読み込む data1 = df.values #pandasの形式からnumpyの形式への変換 X = data1[:,0:2] #説明変数として,0列目と1列めを使う.0:2というのは,0からスタートして2になるまで,なので,0,1列目. y = data1[:,2] #被説明変数として,2列目を使う. |
ダイアログを使って読み込んだのは、あくまでもシステムでファイルを扱えるように読み込んだものです。このプログラムの中では読み込めていません。このプログラムで使えるように、さっき最上部でpandas as pdと書いてpdとしてimportしたpandasを使って、データを読み込みます。pandasにはread_csvという関数があり、それを使ってbinarize.csvを読み込みます。
そして、左から2列を説明変数として、Xに代入します。pythonは数え方が0からスタートするため、0:2列目を読み込め、と書いています。pythonでは、0:2というのは、0からスタートして2になるまで、なので、0列目と1列目という意味です。そして、1番右の列を被説明変数としてYに読み込みます。
|
1 2 3 4 5 |
#しっかりと思ったとおりのデータ形式になっているかチェック.最初の5行くらいのみを,表示の都合上チェックするように. print(data1[0:5,:]) print(X[0:5,:]) print(y[0:5]) print(data1.shape) |
ここは無くてもいいのですが、基本的にビビりなので、ちゃんと作れているか表示しています。最初の5行くらい。また,最後のprint文は,行列の形を調べています.
実行すると,以下のような結果が得られます.
[[5.1 1.5 0. ]
[4.2 3.2 1. ]
[0.7 0.9 0. ]
[1.2 0.7 0. ]
[8.8 1.7 1. ]]
[[5.1 1.5]
[4.2 3.2]
[0.7 0.9]
[1.2 0.7]
[8.8 1.7]]
[0. 1. 0. 0. 1.]
(200, 3)
最初に示したテーブル通りのデータになっていることがわかると思います。よかった。
|
1 2 3 4 5 6 7 |
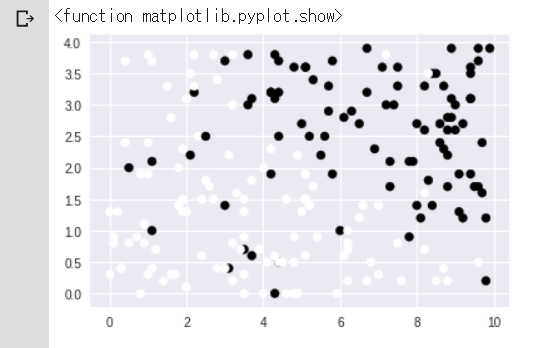
#X1を横軸,X2を縦軸,色の違いがyの値として,どういう分布になっているか確認. %matplotlib inline X1 = X[:,0] X2 = X[:,1] plt.scatter(X1,X2,c=y) plt.show |
説明変数が2つなので、それぞれを横軸、縦軸として、それらとクラスの分布についてプロットしてみました。こんな感じの図になっています.意図的に作ったデータだけあって、まあまあ分かりやすく分布しているものの、ちらちらと例外データもあったりします。
|
1 2 3 4 5 |
from sklearn.model_selection import train_test_split #係数決定のためのデータと,テストのためのデータを分ける関数 X_train, X_test, y_train, y_test = train_test_split(X,y, test_size = 0.2) #20%をテスト用に. print('train size:', X_train.shape[0]) print('test size:', X_test.shape[0]) |
sklearn.model_selectionから,train_test_splitという関数を読み込んでいます.sklearnはscikit-learnといって,Pythonの機械学習用ライブラリです.
こういうfrom … import …みたいなやつは,普通はプログラムの最初に書くんですが,今回は説明用に,関数を使う場所の近所に書きました.
X, yを,それぞれ,学習用8割,テスト用2割,といった分け方をしています.
で,下2行のprint文で,本当に8割,2割になっているか確認しています.
train size: 160
test size: 40
実行すると,確かにそうなっています.
|
1 2 3 4 5 6 7 |
from sklearn.linear_model import LogisticRegression #ロジスティック回帰を行うための関数 lr = LogisticRegression() lr.fit(X_train, y_train) #ここで,計算を行っている. print (lr.intercept_) #計算して得られた切片 print (lr.coef_) #計算して得られた係数 |
次は,sklearnから,ロジスティック回帰を行うための関数LogisticRegressionのインポートを行っています.
で,次の行とその次の行で,X_trainとy_trainという入力と出力の組み合わせを与えることで,それにもっともマッチする係数を出すことができます.lr.fitというのがポイントです.下2行は,それぞれ切片と係数を確かめています.(なお,train_test_splitはランダムで分割するので,以下の結果はランダムで変わります)
[-3.25466321]
[[0.36590136 0.68987314]]
|
1 2 3 4 5 6 7 8 9 10 11 12 |
w_0 = lr.intercept_[0] w_1 = lr.coef_[0,0] w_2 = lr.coef_[0,1] print(w_0) print(w_1) print(w_2) xx1 = np.arange(0,10,0.01) xx2 = (-w_1 * xx1 - w_0)/w_2 plt.plot(xx1,xx2,'-') plt.scatter(X1,X2,c=y) plt.show |
求まった係数をw_0, w_1, w_2に代入します.ちなみに,w_0+w_1*X1+w_2*X2 = 0という関係があります.その線をもとにクラスが分かれます.
で,下半分はプロットのための部分です.np.arange(0,10,0.01)で,0から10まで0.01刻みでxx1を設定します.そして,xx2 = (-w_1 * xx1 – w_0)/w_2という関係のプロットを描いて,上の分布図と合わせます.それが以下の結果ですが,それなりにまっとうなところで分割できている様子がわかります.
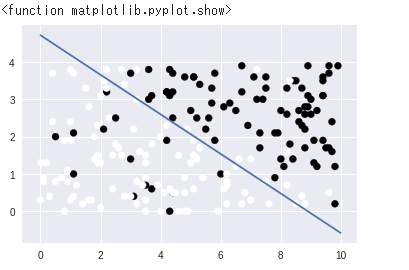
|
1 2 3 |
print(lr.predict(X_test)) #テスト用データを,上で得られた式に入れた結果 print(y_test)#テスト用データの正解 print(lr.score(X_test,y_test))#何割正解したか? |
ここでは,テスト用に確保してあったX_testを,先程作ったモデルに入れたらどうなるかということを確認しています.
lr.predictとすれば,予測をしてくれます.で,テスト用データの正解と比較した正解率を,lr.scoreで出してくれます.
|
1 2 3 4 5 6 7 8 9 10 |
#最後の2割だけでは物足りないので,交差検証をして,全体的にどうなっているか調べてみる. from sklearn.model_selection import StratifiedKFold, cross_val_score #StratifiedKFoldはK分割交差検証用 stratifiedkfold = StratifiedKFold(n_splits=8) #K=8分割 scores = cross_val_score(lr, X, y, cv=stratifiedkfold) # 各分割におけるスコア print('Cross-Validation scores: {}'.format(scores)) # スコアの平均値 print('Average score: {}'.format(np.mean(scores))) |
とはいえ,後ろ2割を引っ張ってきても全体が合っているかどうかこころもとないので,ここでは交差検証を行っています.
Wikipediaによれば,交差検証とは,統計学において標本データを分割し、その一部をまず解析して、残る部分でその解析のテストを行い、解析自身の妥当性の検証・確認に当てる手法を指す...らしいです.というか実際にそうです.特に,K分割交差検証というのをここではやりました.StratifiedKFoldというのはその関数です.で,ここではK=8としています.つまり,標本群を8個に分割し,そのうち7つを用いて学習を行い,そして残り1つをテストデータとして精度を評価する,というのをテストデータを変えながら8回繰り返しています.
以下はその結果を示しています.
Cross-Validation scores: [0.84615385 0.80769231 0.76923077 0.8 0.84 0.875
0.95833333 0.79166667]
Average score: 0.8360096153846154
最初の行列は8回それぞれの正解率,最後はその平均です.だいたい83.6%の正解率であることがわかります.